A Christmas tree spread with calls is an advanced options strategy that consists of three legs and six total options. The option strategy involves buying one call at strike price A, skipping strike price B, selling three calls at strike price C, and then buying two calls at strike price D. It is somewhat similar to a butterfly spread, where the desired outcome is a pin at the short middle strikes, but given a more room to run on the upside, thus a more bullish option strategy.
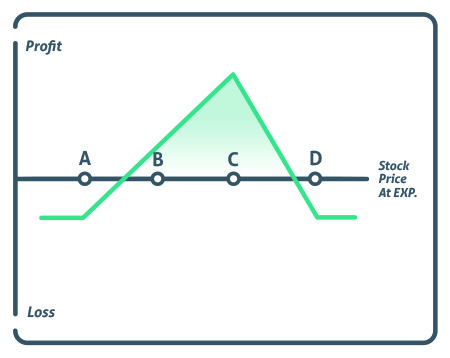
Costs are also higher versus a standard butterfly spread due to the long lower legged strike price that is further away from the short middle strikes. Because the position is opened at a higher cost, the stock must move higher to become profitable. Although it does have a higher probability of a loss, in the event the stock does move against the trader, losses are capped at the opening price.
Profit/Loss
The maximum profit is calculated by taking the difference between the lowest strike price and the three short middle call strike price, then subtracting the cost of the trade. For example, if the distance between point A and C was $10 and the trade cost $2.50, then the max profit would be $7.50.
The maximum loss would be the cost of the trade, so with the same example, the maximum loss would be $2.50.
Breakeven
There are two breakeven points. The lower breakeven point would be calculated by taking the bottom strike price (point A) and adding the cost of the trade. So if point A was a 90-strike price option, and the trade cost $2.50, the lower breakeven would be $92.50.
The upper breakeven point would be calculated by taking the highest strike price (point D) and subtracting one-half of the net debit. So, if the point D strike price was equal to $105 and the cost of the trade was $2.50, then our upper breakeven would be 103.75 (105-2.50/2).
Example
If XYZ is trading $90 and is expected to trade higher over the next three months, a trader could execute a 90/100/105 Christmas tree spread by buying one 90-strike price call, selling three 100-strike price calls, and buying two 105-strike price calls for the following prices:
- Buy 1 XYZ 90-strike price call for $8.00
- Sell 3 XYZ 100-strike price calls for $6.90 ($2.30 each)
- Buy 2 XYZ 105-strike price calls for $1.40 ($.70 each)
- Total cost = $2.50
If the stock trades down over the next three months, the investor will have lost his full $2.50, and all positions will be removed from his account.
If the stock trades up to $100 at expiration, then the trader will gain $10 on the stock movement, capitalizing on the 90-strike price option, while the rest of the options expire worthless. Because they paid $2.50 for the trade, their net profit would be $7.50.
If the stock traded up to $110, the investor would make $20 on the $90 call. Lose $10 X3 on the short middle 100-calls for a total of $30. Gain $5 X2 on the long upper 105-calls for a total of $10.
The net result would be $20 – $30 + $10, which mean all the profits are a wash, but because the investor paid $2.50 for the trade, their net loss is $2.50.
Conclusion
The higher a trader sets the strike prices, the more bullish a Christmas Tree spread becomes, while at the same time, reducing the cost of the trade. However, the higher the strike prices are set, the lower the probability of success.
This type of spread is sensitive to changes in implied volatility. The net price of the spread drops when implied volatility rises and the price increases when implied volatility falls, meaning it has an inverse relationship to implied volatility changes. The trader who executes this trade wants a drop to implied volatility.
This is not a strategy for a beginner, only experienced traders should execute a Christmas tree spread options strategy.



